
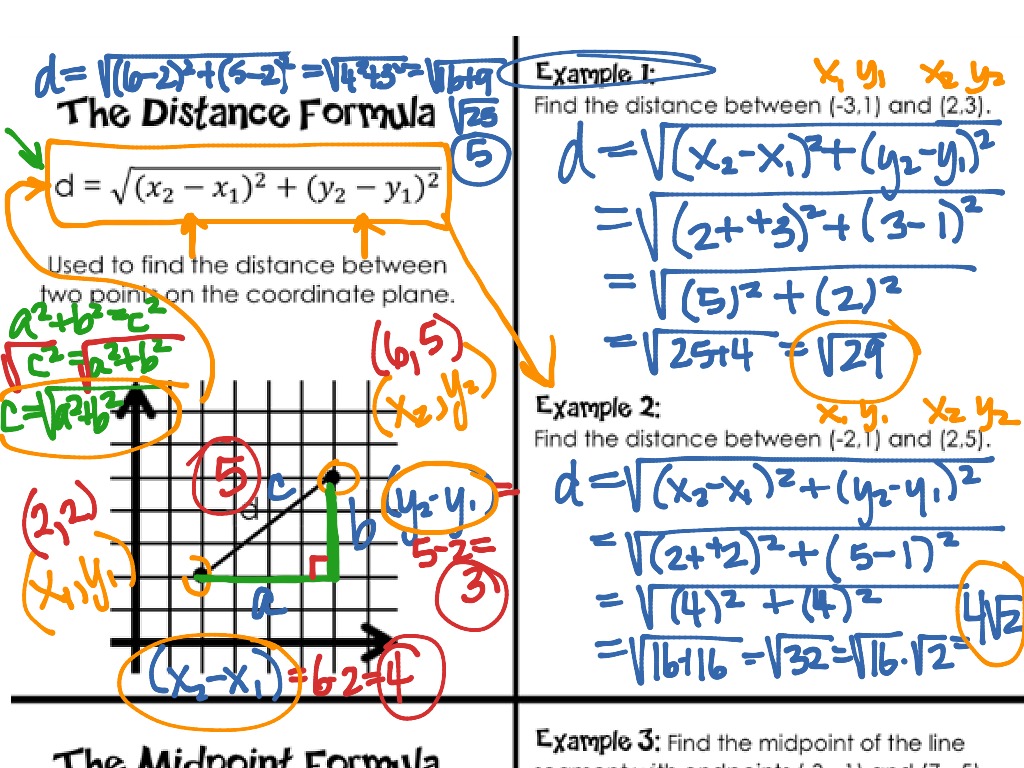
Here, a and b are legs of a right triangle and c is the hypotenuse. ( (x1,y1) ) are the coordinates of point A, and ( (x2,y2) ) are the coordinates of point B. The distance between any two parallel lines is the perpendicular distance from any point on one line to the other line. (x - x)² + (y - y)², which relates to the Pythagorean theorem: a² + b² c². As one of the mechanical proofs of the Pythagorean theorem shows, the same is also true in physics, although in either science it's not the only distance formula used. Consider an XY plane with two points A and B. In mathematics, the Euclidean distance is most fundamental. In a city, one often finds that the taxicab distance formula There are buildings, streets busy with traffic, fences and what not, to be accounted for. Indeed, in a city - just to take one example - it is often impossible to move from one point straight to another. In the haversine formula, d is the distance between two points along a great circle, r is the radius of the sphere, 1 and 2 are the latitudes of the two. If the question is, How fast you can get from one point to another while moving at a given speed, the Euclidean formula may not be very useful providing the answer. In the plane - since the Earth is round, this means within relatively small areas of Earth's surface - it is pretty good, provided the distance is exactly what you want to estimate. How good is the (Euclidean) distance formula for measuring real distances? This depends on the circumstances. The notes also include the formulas and sample problems for finding the midpoint between two points on a number line and on a coordinate plane. This is of course always the case: the straight line segment whose length is taken to be the distance between its endpoints always serves as a hypotenuse of a right triangle (in fact, of infinitely many of them. This set of guided notes gives formulas and sample problems for the distance between two points on a number line and on a coordinate plane.
#Distance formula geometry plus
This side squared plus that side squared is equal to hypotenuse squared, because this is a right triangle. Sometimes people will call this the distance formula. Which gives the length of the hypotenuse as 5, same as the distance between the two points according to the distance formula. The distance formula is a formula that is used to find the distance between two points. The distance squared is going to be equal to this delta x squared, the change in x squared plus the change in y squared. By the Pythagorean theorem, the square of the hypotenuse is (hypotenuse)² = 3² + 4². With this small addition we get a right-angled triangle with legs 3 and 4. The horizontal distance between the points is 4 and the vertical distance is 3. This formula is actually extracted from the Pythagorean Theorem as it is written below: a2+b2d2 a2 + b2 d2. Question 2: The coordinates of point A are (1,7) and the coordinates of point B are (3,2). The distance PQ between two points P(X1,Y1) & Q(X2,Y2) is PQ (X1 -X2)2 +(Y1 - Y2)2 which is called distance formula in Coordinate Geometry. To measure the distance between two points in an orthogonal coordinate system, we use a formula that is very important in geometry.

Hence, according to the Distance Formula, the distance between points A and B is 5 units. Find the distance between these two points. The source of this formula is in the Pythagorean theorem. Question 1: The coordinates of point A are (-4,0) and the coordinates of point B are (0,3). According to the Euclidean distance formula, the distance between two points in the plane with coordinates (x, y) and (a, b) is given byĪs an example, the (Euclidean) distance between points (2, -1) and (-2, 2) is found to be

Suppose \(P(x_1,y_1)\) and \(Q(x_2,y_2)\) are two points in the number plane.Very often, especially when measuring the distance in the plane, we use the formula for the Euclidean distance.

We can construct a right-angled triangle \(ABC\), as shown in the following diagram, where the point \(C\) has coordinates \((a,d)\).Ī similar formula applies to three-dimensional space, as we shall discuss later in this module. In coordinate geometry, the way to find the distance between two. Want to learn more about the distance formula Check out this video. One formula to bring them all, and in the darkness bind them. In order to derive the formula for the distance between two points in the plane, we consider two points \(A(a,b)\) and \(B(c,d)\). The formula gives the distance between two points and on the coordinate plane: It is derived from the Pythagorean theorem. The distance from \(A\) to \(B\) is the same as the distance from \(B\) to \(A\). Distances in geometry are always positive, except when the points coincide.


 0 kommentar(er)
0 kommentar(er)
